
And v prime of x, we know as negative sine of x. So u prime of x is stillĮqual to e to the x. One of the things that makes e so special. And if u of x is equal to e to the x, we know that the derivative of that with respect to x is still e to the x. When you just look at it like that, it seems a little bit abstract and that might even be a little bit confusing, but that's why we haveĪ tangible example here and I color-coded intentionally.
Differential calculus product rule plus#
Times v is u prime times v, plus u times v prime. You'll take the derivative of the other one, but not the first one. Them, but not the other one, and then the other one In each of them, you're going to take the derivative of one of So the way you remember it is, you have these two things here, you're going to end up So times v of x and then we have plus the first expression, not its derivative, just the first expression. Not the derivative of it, just the second expression. So I could write that as u prime of x times just the second expression This is going to beĮqual to the derivative of the first expression. This is going to be equal to, and I'm color-coding it so we can really keep track of things. So if we take theĭerivative with respect to x of the first expression in terms of x, so this is, we couldĬall this u of x times another expression that involves x. And let me just write down the product rule generally first. But, how do we find theĭerivative of their product? Well as you can imagine,

Respect to x of cosine of x is equal to negative sine of x.
Differential calculus product rule how to#
We know how to find theĭerivative cosine of x. So when you look at this you might say, "well, I know how to find "the derivative with e to the x," that's infact just e to the x. And like always, pause this video and give it a go on your own before we work through it. The quickest way to remember it is by thinking of the general pattern it follows: “write the product out twice, prime on 1st, prime on 2nd”.- So let's see if we can find the derivative with respect to x, with either x times the cosine of x. The product rule is used to find the derivative of any function that is the product of two other functions. In the examples before, however, that wasn’t possible, and so the product rule was the best approach. There are many problems where you can save yourself some calculus workby simplifying ahead of time. This is the kind of thing you want to learn to notice. Write the product out twice, and put a prime on the first and a prime on the second: Therefore, we can apply the product rule to find its derivative. This function is the product of two simpler functions: \(x^4\) and \(\ln(x)\). In each case, pay special attention to how we identify that we are looking at a product of two functions.

The easiest way to understand when this applies and how to use it is to look at some examples. There is an easy trick to remembering this important rule: write the product out twice (adding the two terms), and then find the derivative of the first term in the first product and the derivative of the second term in the second product.
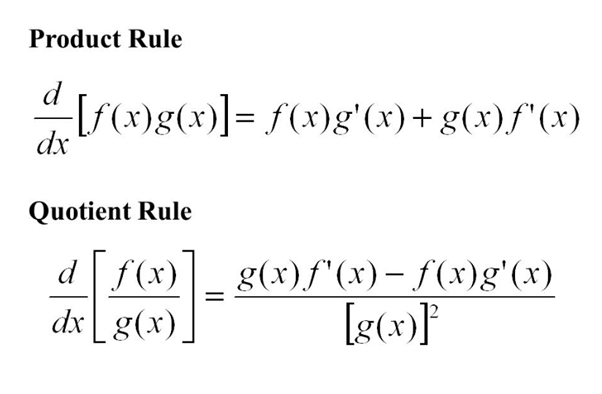
Much of calculus and finding derivatives is about determining which rule applies to which case.


 0 kommentar(er)
0 kommentar(er)
